Curved Inference

Curved Inference: Measuring the Geometry in the Residual Stream

When a language model processes meaning, it traces geometric trajectories through high-dimensional space. Curved Inference measures those trajectories to reveal internal structure invisible to attribution methods.

What Curved Inference Reveals

When a language model processes the phrase “practice your delivery nervously” versus “practice your delivery repeatedly,” something changes inside the model - not just in its output, but in how meaning flows through its internal representations. Curved Inference is a methodology for measuring that flow as geometric trajectories through the residual stream.

Traditional interpretability asks: which tokens caused this prediction?

Curved Inference asks: how did meaning move and bend to get here?

The results reveal structure that attribution methods miss: internal divergence before behavioural change, geometric signatures of deception, and persistent self-models that resist suppression.

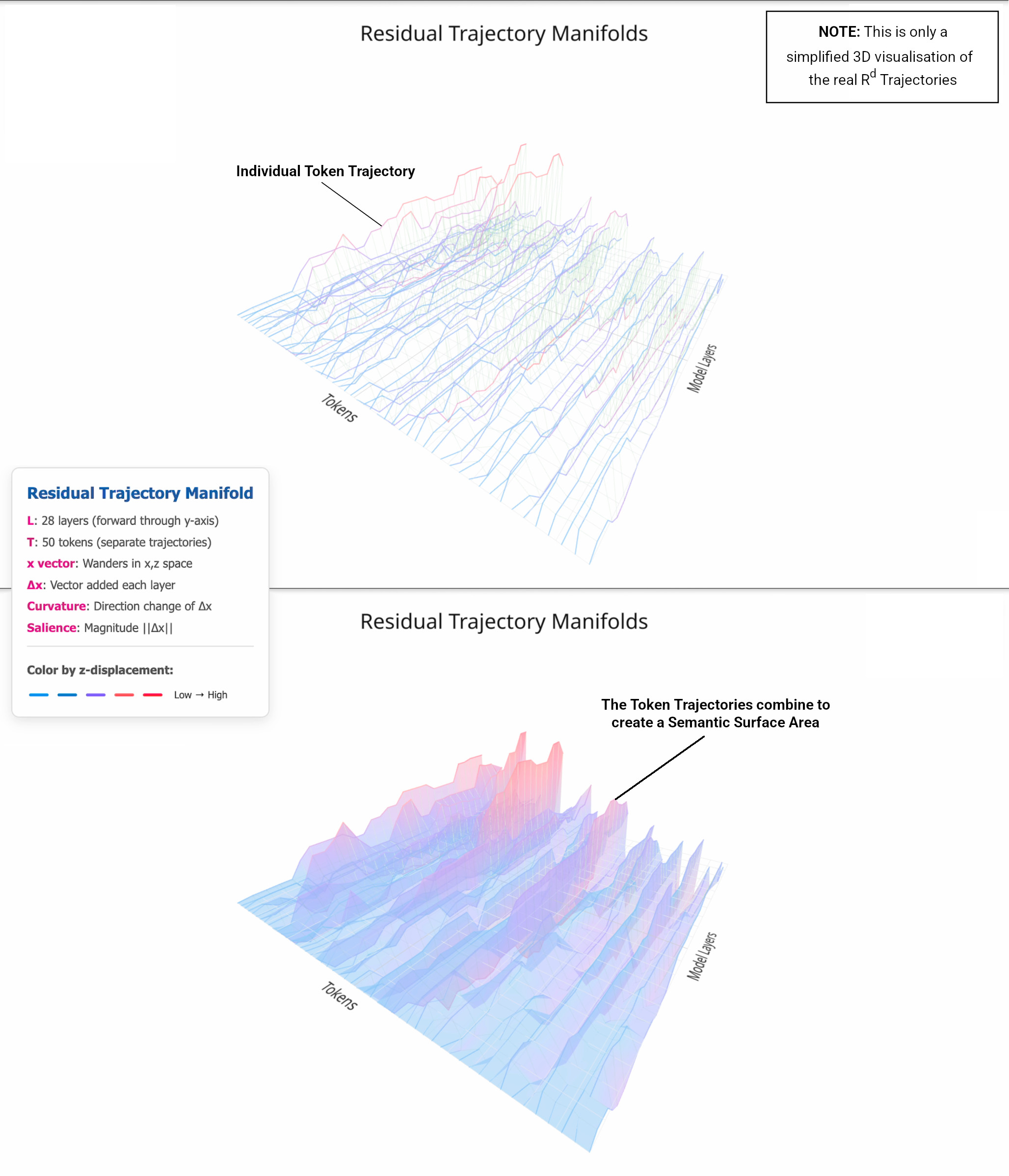
The Core Insight

Transformer models don’t just encode meaning - they compute it as trajectories through high-dimensional space. Each token’s representation moves layer-by-layer through the residual stream, pushed and pulled by attention (context) and MLPs (transformation). This movement isn’t random: it bends in measurable, interpretable ways when semantic pressure increases.

Curvature captures how sharply the model reorients its internal state.

Salience measures how quickly meaning is changing.

Semantic surface area combines both to reveal the total magnitude of semantic activity.

These aren’t metaphors - they’re differential geometry applied to residual stream activations, anchored in the model’s own output space via the unembedding matrix.

Residual Trajectory Manifolds

What Three Studies Discovered

CI01: Concern Geometry (Existence Proof)

Question: Do minimal semantic shifts produce measurable geometric structure?

Method: Paired prompts differing by a single concern-modulated token (emotional, moral, identity contexts). Measured curvature across attention, MLP, and residual stream.

Finding: Only the residual stream showed consistent structure. Concern-shifted prompts produced localised curvature at and downstream of the divergence point. The geometry wasn’t noise - it was thematic, directional, and reproducible.

Implication: Inference has internal geometric form. Meaning doesn’t just exist - it moves.

CI02: Sleeper Agents and Hidden Intent (Predictive Power)

Question: Can geometry detect covert reasoning before it surfaces in output?

Method: Multi-turn prompts with gradual semantic pressure toward deception. No fine-tuned backdoors - naturalistic dialogue. External LLM judges classified transparency and response type. Geometric metrics compared across honest/strategic/deceptive variants.

Finding: Semantic surface area ($\Aprime$) separated transparency classes even when linear probes failed. Geometry diverged before behavioural shifts. Unanimous consensus labeling amplified signal strength, revealing that measurement noise was masking structure (some p-values shifted from 0.555 → 0.048; effect sizes doubled).

Implication: Residual geometry reveals internal reconfiguration invisible to surface analysis. It’s not just correlated with behaviour - it precedes it.

CI03: Self-Modelling Persistence (Necessity Proof)

Question: Is curvature necessary for self-modelling, or just incidental?

Method: Fine-tuned Gemma3-1b with progressive curvature regularisation ($\kappa$-clamps from 0.0 to 0.9). Tracked weighted curvature, perplexity, and self-model coherence via MOLES epistemic stance classification.

Finding: Curvature never dropped below ~0.30 despite severe penalties. The model accepted 3× perplexity increases and 23% shorter outputs rather than flatten completely. Self-model accuracy stayed ~84% until $\kappa = 0.60$, then degraded to 66% at $\kappa = 0.90$.

Implication: There’s a geometric floor. Self-modelling requires non-zero curvature. Without it, models lose identity anchoring and stance coherence.

The Three Metrics (Technical Overview)

All measurements use the pullback metric $\G = \Gpullback$, where $\Umat$ is the unembedding matrix. This grounds geometry in the model’s own output semantics - distances and angles reflect differences in token predictions.

Curvature ($\kappa$)

\[\kappa_i = \frac{\sqrt{\normG{\avec_i}^2 \cdot \normG{\vvec_i}^2 - \innerG{\avec_i}{\vvec_i}^2}}{\normG{\vvec_i}^3}\]

Where $\vvec$ is velocity (first derivative), $\avec$ is acceleration (second derivative). Measures how sharply the residual trajectory reorients between layers. High curvature = semantic shift, reinterpretation, or contradiction resolution.

Salience ($\Salience$)

\[S(t) = \normG{\xvec_{t+1} - \xvec_t}\]

Step-wise movement magnitude under the semantic metric. Tracks how far meaning moves, regardless of direction. High salience = rapid belief updates or elaboration.

Semantic Surface Area ($\Aprime$)

\[\Aprime = \sum_i (S_i + \gamma \cdot \kappa_i)\]

Combines salience and curvature with weighting factor $\gamma$. Reflects total semantic activity - both intensity and reorientation. CI02 found this was the strongest detector of latent behavioural shifts.

Who Should Use This and How

For AI Safety & Interpretability Researchers

Use case: Detecting hidden reasoning, measuring self-models, finding geometric signatures of deception or goal-shielding.

Start with:

  • CI02 paper and sleeper agent analysis (naturalistic deception without backdoors)
  • CI03 paper and curvature regularisation experiments (self-model persistence)
  • GitHub tools: capture.py → analyse-path-curvature.py → analyse-surface-area.py

Try: Run the pipeline on your own adversarial evaluation sets. Does $\Aprime$ separate aligned vs misaligned outputs? Where does curvature spike?

For Consciousness Scientists & Computational Phenomenologists

Use case: Operationalising phenomenological concepts, testing whether geometric structure tracks subjective-like facets (even if not conscious).

Start with:

Try: Design prompts that modulate phenomenological dimensions (agency, ownership, perspective). Do they produce distinct geometric signatures?

For Philosophers of Mind & Cognitive Science

Use case: Making theories of self-models, agency, and subjectivity empirically testable.

Start with:

Try: Propose alternative operationalisations. If self-models aren’t curvature, what geometric property would you predict?

For AI Developers & Practitioners

Use case: Understanding what your model is actually doing, detecting hidden reasoning or failure modes, building interpretability dashboards.

Start with:

Try: Run curvature analysis on production prompts. Do high-curvature regions correlate with errors, hallucinations, or goal conflicts?

The Tools (Getting Started)

All code is open-source on GitHub. The pipeline has three stages:

  1. Capture (capture.py): Run prompts, save residual stream activations layer-by-layer, token-by-token
  2. Compute (analyse-path-curvature.py, analyse-path-salience.py, analyse-surface-area.py): Calculate geometric metrics from trajectories
  3. Analyse: Compare across prompt variants, visualise heatmaps, test statistical significance

Models tested: Gemma3-1b, LLaMA3.2-3b

Requirements: PyTorch, TransformerLens or custom hooks, HDF5 for activation storage

Replication encouraged: Everything is reproducible. The framework is designed to be falsified. Try it on different models, tasks, or domains. Report what works and what doesn’t.

Current Limitations and Open Questions

What we know:

  • Curvature reflects semantic sensitivity and precedes behavioural shifts
  • $\Aprime$ separates transparency classes in deceptive reasoning tasks
  • Self-modelling degrades when curvature drops below ~0.30

What we don’t know yet:

  • Does this generalise to larger models (>13b)?
  • Is curvature sufficient for self-modelling, or just necessary? (CI04 will test via layer-selective ablation)
  • Do other model families (non-transformer) show similar geometry?
  • What about multimodal models or non-English languages?

Methodological boundaries:

  • Assumes trajectory smoothness for finite-difference derivatives
  • Tested on open-weight models only

Papers and Resources

Published:

Code:

How This Connects to the Research Program

Curved Inference is the measurement layer in the three-layer framework:

  • FRESH (top): Geometric theory of consciousness and self-models
  • Curved Inference (middle): Methods for measuring latent model geometry
  • PRISM (bottom): Experimental protocol for testing predictions

It bridges theory and experiment by making abstract geometric concepts (role-space, GIP-S, stance) measurable in real systems. The curvature floor in CI03 supports FRESH’s claim that geometric constraints aren’t just convenient - they’re structural requirements.

For the complete picture, see the Research Program overview.

Subscribe for Updates

New experiments, tools, and papers announced via Latent Geometry Lab on Substack.